Centrage

Le centrage c’est presque simple !
Thierry Platon
21/09/2006

Rappels d’aérodynamique

Selon la théorie linéaire des profils minces, l'action de l'écoulement de l'air sur le profil d’une aile se traduit par :

- une force de portance Pa = 1/2.r.S.V². perpendiculaire à la vitesse air et appliquée en un point F appelé foyer du profil.

r : masse volumique de l’air

S : surface

V vitesse air

Lorsqu’on est loin du décrochage (c’est à dire pour des incidences pas trop élevées), le coefficient de portance dépend de l'incidence a du profil selon une loi linéaire :

Cza(a) =(a- a0) avec = (cas d’une aile avec répartition elliptique de portance)

En première approximation est une constante indépendante du profil ,

est l’allongement de l’aile,

a0 est l'angle d'incidence à portance nulle du profil.

- une force de traînée T= 1/2.r.S.V².Cx opposée à la vitesse air

Cx : coefficient de traînée

- un moment de rotation M = 1/2.r.C.S.V².Cm qui a tendance à faire pivoter le profil.

Cm : coefficient de moment,

C : corde du profil

Le coefficient de moment Cm est intimement lié à la courbure du profil. Il est nul pour les profils symétriques, négatif (c'est-à-dire piqueur) pour les profils classiques, positif (c'est-à-dire cabreur) pour les profils autostables (ailes volantes).

Selon la théorie des profils minces, lorsque le foyer F est positionné à 25% de la corde, le coefficient de moment Cm devient indépendant de l'incidence.

On a alors Cm = cte = Cm0, moment à incidence nulle

Centre de poussée du profil

En prenant le bord d’attaque comme référence, le moment total auquel est soumis le profil est la somme du moment du à la portance et du moment M:

Mtotal = 0,25.C.P – M = 1/2.r.S.V².C.(0,25Cz – Cm) = 1/2.r.S.V².Cz (0.25 – Cm/Cz)

Mtotal = P (0.25 - Cm/Cz).C

L'effet combiné de la portance P appliquée au foyer F et du moment M est donc équivalent à celui de la seule force de portance appliquée en un point appelé « centre de poussée» ( CP ) et défini par la relation :

Xcp = 0.25-Cm/Cz La position du centre de poussée dépend du Cz de vol.

Foyer du profil

Il est fondamental de bien distinguer le rôle du centre de poussée CP de celui du foyer aérodynamique F. Une manière simple de se représenter les choses est la suivante : pour un profil soumis à un écoulement d'incidence a :

- Le CP est le point où s'applique l'ensemble des efforts aérodynamiques auquel est soumis le profil, c'est-à-dire la combinaison de la portance Cz et du moment Cm

- Le foyer F est le point où s'applique les seules variations de portance DCz lorsque à partir de l'incidence a le profil subit une variation d'incidence Da.

Contrairement au centre de poussée, la position du foyer F est fixe et indépendante du Cz et de l’incidence. Le foyer est situé à 25% de la corde moyenne en partant du bord d'attaque.

Xf = 0.25 = constante

Il faut cependant préciser que la théorie linéaire des profils minces n’est qu’une approximation. Dans "la vraie vie" Cza et Cm ne sont pas des constantes parfaites mais peuvent varier légèrement avec l'incidence (des logiciels élaborés comme Xfoil/Profili montrent que les courbes Cz= f(α) ne sont pas toujours des droites). En cas de variation du Cm entre deux Cz de vol différents, la position du foyer correspondant dépend de la pente de la courbe Cm = f(Cz) :

Xf = 0.25-DCm/DCz

Foyer du planeur

Pour un planeur complet la définition du foyer aérodynamique est identique:

Le foyer du planeur est le point où s'applique la variation de portance auquel sera soumis le planeur lorsque celui-ci subit une variation d'incidence.

Il est important de noter que l'incrément de portance dont il est question ici est bien la somme de l’incrément de portance de l'aile et de celui du stab. Le foyer du planeur complet est donc situé au barycentre de ces 2 incréments.

Etude de l’équilibre du planeur

Lorsque le planeur est en vol rectiligne uniforme, les forces auxquelles il est soumis s’équilibrent. La somme des forces de portance de l’aile et du stab est équivalente à une force unique appliquée au centre de poussée global du planeur CPglobal. Cette force compense le poids du planeur.

Pa + Ps = mg

Pour que le planeur soit à l’équilibre il faut que le centre de poussée global CPglobal et le centre de gravité du planeur coïncident. Le moment de la portance de l’aile par rapport au centre de gravité (produit de la portance de l’aile par le bras de levier entre CPaile et CG,) est alors équilibré par le moment lié à la portance du stab (produit de la portance du stab par le bras de levier entre CG et le foyer du stab -- on suppose ici un stab symétrique--). Ceci s’écrit :

Pa.(Xcg-Xcp).C = Ps.(L+(0.25-Xcg)C)

Avec Pa : portance de l’aile

Ps : portance du stab on a aussi XCPglobal = Xcg

C : corde aérodynamique moyenne de l’aile

Xcg : position relative du centre de gravité

XCPaile : position relative du centre de poussée de l’aile, XCPaile = 0.25 – Cm/Cza

Soit :

Pa.(Xcg - (0.25 – Cm/ Cza).C = Ps.(L+(0.25-Xcg).C)

On a par ailleurs :

Pa= ½.ρ.V²Sa.Cza et Pstab = ½.ρ.V²Ss.Czs

On peut donc écrire :

Sa.Cza.(Xcg - (0.25 – Cm/ Cza).C = Ss.Czs.(L+(0.25-Xcg)C)

Sa.Cza.(Xcg - (0.25 – Cm/ Cza) = Ss.Czs.(L/C+(0.25-Xcg)

C'est-à-dire (1) :

XCG.(Sa.Cza+ Ss.Czs = (0.25+L/C).Ss.Czs + 0.25.Sa.Cza - Cm.Sa

Comme à l’équilibre Xcg = Xcpglobal, On peut aussi écrire :

XCPglobal.(Sa.Cza+ Ss.Czs) = (0.25+L/C).Ss.Czs + 0.25.Sa.Cza - Cm.Sa

Cette formule plus générale est également valable hors équilibre. Elle exprime le fait que le moment de l’ensemble des efforts aérodynamiques (par rapport à un point de référence situé au bord d’attaque) est égal à la somme :

- du moment associé à la portance du stab appliqué au foyer du stab : (0.25+L/C).Ss.Czs

- du moment associé à la portance de l’aile appliqué au foyer de l’aile : 0.25.Sa.Cza

- d’un moment constant lié au Cm de la voilure : - Cm. Sa

Notion de stabilité

Il est fondamental de bien distinguer la notion de stabilité de la notion d’équilibre définie ci-dessus. La stabilité d’un système ne peut être étudiée que si celui-ci est en équilibre ; cet équilibre peut alors être stable, instable ou neutre :

- un système est dit en équilibre stable s'il a tendance à revenir de lui-même à sa position initiale lorsqu'on l'en écarte. C'est le cas d'une bille au fond d'une surface concave (un bol).

- un système est dit en équilibre instable si, après l'avoir légèrement écarté de sa position initiale, il a de lui-même tendance à s'en éloigner encore plus. C'est le cas de la bille posée au sommet d'une surface convexe (un ballon).

- un système est dit en équilibre neutre si, lorsqu'on l'écarte de sa position initiale, il reste alors dans la nouvelle position où on l'a mis. C'est le cas d'une bille posé sur un plan horizontal. Toutes les positions du plan sont alors des positions d'équilibre.

Considérons un planeur subissant une perturbation quelconque (à coup sur le manche, turbulence, mise en piqué …). Cette perturbation génère une variation d'incidence et donc une variation de portance DCz appliqué au foyer du planeur Fp. Le comportement du planeur après perturbation va dépendre de la position du foyer Fp par rapport au centre de gravité du planeur CG

- soit CG est situé en avant de Fp et le planeur est alors soumis à un moment de tangage qui va le faire revenir vers sa position d'équilibre initiale. Le planeur remonte dans le test du piqué, on dit qu’il est « centré avant ». Il est stable.

- soit CG est situé en arrière du foyer Fp et le planeur est soumis à un moment qui va l'écarter encore plus de sa position initiale. Dans le test du piqué le planeur accentue son piqué initial, il est instable. Il est dit « centré arrière ».

- soit CG et Fp coïncident. Après la perturbation le planeur reste équilibré, il conserve donc sa nouvelle attitude de vol (pas de moment de tangage) ainsi que sa nouvelle incidence. Dans le test du piqué il conserve sa pente de descente, le planeur est dit « neutre »

On notera que, contrairement à la notion d’équilibre, la notion de stabilité ne fait pas intervenir la position du CP de l'aile mais uniquement celle foyer aérodynamique du planeur.

Le foyer est parfois appelé "limite de centrage arrière", je trouve cependant cette appellation assez ambiguë :

- le terme "limite" laisse penser qu'il va se passer quelque chose de vraiment catastrophique si on franchit cette "limite"et que le planeur sera totalement incontrôlable. Ceci n’est pas toujours vrai.

- le terme «limite de centrage arrière» laisse entendre que l’on est déjà centré arrière bien avant d'atteindre cette « limite » qu'il ne faut surtout pas dépasser!

Il faut dire que le terme « foyer du planeur » n'est pas non plus très explicite, l’appellation « point neutre » ou « point de stabilité neutre » serait plus appropriée.

Le centrage « neutre » au foyer du planeur est souvent recherché en voltige ou en vol de pente. Il permet de «poser» le planeur sur une trajectoire qu'il conservera tant qu'aucun ordre ne sera donné. Par contre sur les planeurs de gratte ou de vol à voile, avec lesquels on vole plus haut et plus loin, on adoptera plus volontiers un centrage plus avant. Le planeur sera ainsi stable, revenant de lui-même vers son point de vol après une perturbation. Ce point de vol pourra de plus être optimisé pour que le planeur présente par exemple une finesse maximale ou une vitesse de chute minimale

Calcul simplifié du foyer du planeur

Soit un planeur en vol équilibré qui subit une perturbation Da,

- L’incrément de portance de l’aile est :

DPa = 1/2.r.Sa.V².DCza ( Sa surface de l’aile)

avec DCza = et = ( est l’allongement de l’aile)

Cet incrément de portance s’applique au foyer de l’aile, soit 25% de la corde aérodynamique moyenne de l’aile

On néglige dans un premier temps l’interaction du sillage de l’aile avec le stab. Celui-ci est donc soumis à la même variation d’incidence que l’aile, la variation de portance du stab est donc :

DPs = 1/2.r.Ss.V².DCzs (Ss surface du stab)

avec DCzs = et = ( est l’allongement du stab)

Cet incrément s’applique au foyer aérodynamique du stab.

- Le foyer global du planeur se situe au barycentre de ces 2 incréments (c'est-à-dire le point d’équilibre de ces 2 forces). Sa distance relative par rapport au bord d’attaque de l’aile est donc définie par la relation :

DPa.(Xf – 0.25).C = DPs.(L – (Xf – 0.25).C) (1)

D’où Xf = soit Xf =

De cette formule générale on peut déduire quelques formules simplifiées connues par ailleurs :

- en négligeant la surface de stab au dénominateur on obtient Xf =

Soit en faisant apparaître le volume de stab : Xf ≈

- en admettant que on a alors

Xf ≈

Si dans cette formule on néglige la surface de stab au dénominateur on obtient :

Xf ≈

Cette formule figure (avec une erreur de signe au numérateur) dans l’article sur la méthode SPP sur le site épervier sud Luberon.

On voit ainsi que la position du foyer dépend principalement du volume de stab et des allongements respectifs de l’aile et du stab. Du fait des approximations faites ci-dessus les caractéristiques du profil n’interviennent plus dans cette formule.

Prise en compte du sillage de l’aile

Dans les calculs précédents nous n’avons pas pris en compte l’influence du sillage de l’aile, or celle-ci n’est pas négligeable.

La portance de l’aile génère un effet de sillage qui dévie l’écoulement vers le bas. Un stab calé à zéro sera ainsi soumis à un flux dévié vers le bas et sera en fait légèrement déporteur. Cet effet doit être pris en compte lorsqu’on calcule le calage du stab et la position du foyer.

La déflexion de sillage « e » est proportionnelle au Cz l’aile et dépend de la position du stab par rapport à l’aile. La théorie de la ligne portante donne une valeur de cette déflexion :

e = =

k est ici un coefficient empirique qui permet de tenir compte de la position relative du stab par rapport à l’aile. Les valeurs admises sont les suivantes : k≈ 0.5 pour un stab en T , k≈1 pour un stab situé au même niveau que l’aile. A mon avis ces valeurs demandent à être consolidées de manière expérimentale.

L’incidence vrai au niveau du stab est donc αstab= α – e

Et l’incrément de portance du stab correspondant à une perturbation Da est :

DPs = 1/2.r.Ss.V².DCzs = 1/2.r.Ss.V².As (Da -De) = 1/2.r.Ss.V².(1-).As Da

Dans le calcul de cet incrément de portance tout se passe donc comme si le coefficient de portance du stab As était multiplié par

1- = 1 - .

La position du foyer est donc définie par :

Xf = avec ε =

Cette formule est analogue à celle proposée par Jean Couzinet et citée par Serge Barth dans Looping n°59. Le coefficient K utilisé par Jean Couzinet a donc pour valeur K =

En négligeant la surface de stab au dénominateur on obtient une formule simplifiée:

Xf = ,

Soit en introduisant le volume de stab Xf ≈

avec =

Cette formule figure dans l’article sur le centrage sur le site de Matthieu Scherrer

Prise en compte des variations de Cm

Nous avons vu qu’en cas de variation du coefficient de moment Cm, la position du foyer du profil est

Xfprofil = 0.25 -

L’équation (1) devient alors :

DPa.(Xf – (0.25-).C = DPs.(L – (Xf – 0.25).C)

On en déduit la position du foyer global du planeur :

Xf = -

D’où la formule suivante prenant en compte la variation de Cm :

Xf = -

Avec = = ε =

Cette formule permet notamment de prendre en compte l’influence du profil et des variations de et de Cm sur la stabilité du planeur en fonction du régime de vol

Prise en compte de la portance du fuselage

Même en ne faisant aucune approximation et en tenant compte des corrections liées au sillage de l’aile et aux variations de Czα et de Cm, la position du foyer donnée par les calculs ci-dessus est en général sensiblement plus reculée que celle que l’on peut mesurée après avoir parfaitement réglé son planeur pour avoir un comportement neutre. Nous avons supposé que cet écart pouvait être lié à la portance du fuselage. Voici donc une approche qui permet de prendre en compte une correction de fuselage.

Soit Lf, la longueur du fuselage, Sf sa surface projetée dans le plan horizontal, et Xav la longueur relative de l’avant du fuselage (rapport entre la distance nez - BA emplanture et la longueur du fuseau). On admet que la portance du fuselage est proportionnelle à Sf ainsi qu’à un coefficient de portance Af. On suppose également que le foyer du fuselage se situe à une distance relative Xfus du nez du planeur.

En introduisant l’incrément de portance fuselage ΔPf, l’équation (1) devient :

DPa.(Xf – 0.25).C + ΔPf.(0.25+(Xav – Xfus).Lfus + Xf.C) = DPs.(L – (Xf – 0.25).C)

Avec ΔPf = Sf. Af. Da

On en déduit la position du foyer Xf

Xf =

Soit la formule générale suivante :

Xf = 0.25 +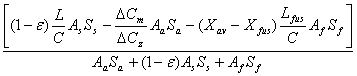

Avec = = ε =

Il n’existe pas de formule pour calculer les paramètres Xfus (position relative du foyer fuselage) et Af (coefficient de portance du fuselage). Nous proposons donc une approche purement empirique en définissant un jeu de valeur (Xfus, Af) à partir de la mesure du centre de gravité sur des modèles réels.

Xfus ≈ 0.2 et Af ≈ 0.08 (l’incidence alpha étant exprimé en degré)

( ces valeurs restent à optimiser et à valider )

Feuille de calcul Excel

Une feuille de calcul Excel a été développée pour faciliter la mise en œuvre de ces formules. Ce fichier Excel permet les calculs de centrage pour des planeurs ayant des géométries aile et stab en simple trapèze. Ce fichier est encore en cours de validation. Dans ce but j’aurais besoin d’avoir les caractéristiques de planeurs très différents (envergures et profils différents, stab en croix, stab en T, fuselage fin ou au contraire volumineux , nez court ou long…etc). Merci donc à ceux qui voudraient participer à cette validation de se mettre en contact avec moi.

A suivre donc après validation de ce fichier……